МОДЕЛИ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ

07.04.2007, 13:21

Notice: Undefined variable: pageadd in /home/u00372/public_html/top_add.php on line 36

Продукционная модель

"Продукционная модель, или модель, основанная на правилах, позволяет представить знания в виде предложений типа: Если (условие), то (действие)."

Под условием понимается некоторое предложение-образец, по которому осуществляется поиск в базе знаний, а под действием - действия, выполняемые при успешном исходе поиска (они могут быть промежуточными, выступающими далее как условия, и терминальными или целевыми, завершающими работу системы).
При использовании продукционной модели база знаний состоит из набора правил. Программа, управляющая перебором правил, называется машиной вывода. Чаще всего вывод бывает прямой (от данных к поиску цели) или обратный (от цели для ее подтверждения - к данным). Данные - это исходные факты, на основании которых запускается машина вывода - программа, перебирающая правила из базы.
Пример. Имеется фрагмент базы знаний из двух правил:
П1: Если "отдых - летом" и "человек - активный", то "ехать в горы".
П2: Если "любит солнце", то "отдых летом".
Предположим, в систему поступили данные - "человек активный" и "любит солнце".
Прямой вывод - исходя из данных, получить ответ.
1-й проход.
Шаг 1, Пробуем П1, не работает (не хватает данных "отдых - летом").
Шаг 2. Пробуем П2, работает, в базу поступает факт "отдых - летом".
2-й проход.
Шаг 3. Пробуем П1, работает, активируется цель "ехать в горы", которая и выступает как совет, который дает ЭС.
Обратный вывод - подтвердить выбранную цель при помощи имеющихся правил и данных.
1-й проход.
Шаг 1. Цель - "ехать в горы": пробуем П1 - данных "отдых - летом" нет, они становятся новой целью, и ищется правило, где она в правой части.
Шаг 2. Цель "отдых - летом": правило П2 подтверждает цель и активирует ее.
2-й проход.
Шаг 3. Пробуем П1, подтверждается искомая цель.
Продукционная модель чаще всего применяется в промышленных экспертных системах. Она привлекает разработчиков своей наглядностью, высокой модульностью, легкостью внесения дополнений и изменений и простотой механизма логического вывода.
Имеется большое число программных средств, реализующих продукционный подход (язык OPS 5; "оболочки" или "пустые" ЭС - EXSYS, ЭКСПЕРТ; инструментальные системы ПИЭС и СПЭИС и др.), а также промышленных ЭС на его основе (ФИАКР) и др.

Семантические сети

Термин семантическая означает смысловая, а сама семантика - это наука, устанавливающая отношения между символами и объектами, которые они обозначают, т.е. наука, определяющая смысл знаков.

"Семантическая сеть - это ориентированный граф, вершины которого - понятия, а дуги - отношения между ними."

Понятиями обычно выступают абстрактные или конкретные объекты, а отношения - это связи типа: "это" ("is"), "имеет частью" ("has part"), "принадлежит", "любит". Характерной особенностью семантических сетей является обязательное наличие трех типов отношений:

класс - элемент класса;

свойство - значение;

пример элемента класса.
Можно ввести несколько классификаций семантических сетей. Например, по количеству типов отношений:

однородные (с единственным типом отношений);

неоднородные (с различными типами отношений).
По типам отношений:

бинарные (в которых отношения связывают два объекта);

n-арные (в которых есть специальные отношения, связывающие более двух понятий).
Наиболее часто в семантических сетях используются следующие отношения:

связи типа "часть-целое" ("класс-подкласс", "элемент-множество" и т.п.);

функциональные связи (определяемые обычно глаголами "производит", "влияет"...);

количественные (больше, меньше, равно...);

пространственные (далеко от , близко от, за, под, над ...);

временные (раньше, позже, в течение...);

атрибутивные связи ( иметь свойство, иметь значение...);

логические связи (и, или, не) и др.
Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети, соответствующей поставленному вопросу. Пример. На рисунке изображена семантическая сеть. В качестве вершин - понятия: Человек, Иванов, Волга, Автомобиль, Вид транспорта, Двигатель.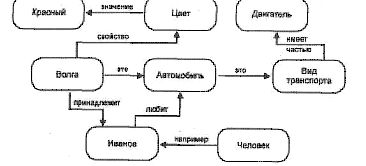


Основное преимущество этой модели - в соответствии современным представлениям об организации долговременной памяти человека. Недостаток модели - сложность поиска вывода на семантической сети.
Для реализации семантических сетей существуют специальные сетевые языки, например NET и др.
Широко известны экспертные системы, использующие семантические сети в качестве языка представления знаний - PROSPECTOR, CASNET, TORUS.

Фреймы

Фрейм (англ. frame - каркас или рамка) предложен М.Минским в 70-е гг. как структура знаний для восприятия пространственных сцен. Эта модель, как и семантическая сеть, имеет глубокое психологическое обоснование.
Под фреймом понимается абстрактный образ или ситуация. В психологии и философии известно понятие абстрактного образа. Например, слово "комната" вызывает у слушающих образ комнаты: "жилое помещение с четырьмя стенами, полом, потолком, окнами и дверью, площадью 6 - 20 м2". Из этого описания ничего нельзя убрать (например, убрав окна, мы получим уже чулан, а не комнату), но в нем есть "дырки", или "слоты", - это незаполненные значения некоторых атрибутов - количество окон, цвет стен, высота потолка, покрытие пола и др.
В теории фреймов такой образ называется фреймом. Фреймом называется также и формализованная модель для отображения образа.
Структуру фрейма можно представить так:
ИМЯ ФРЕЙМА :
(имя 1-го слота: значение 1-го слота),
(имя 2-го слота: значение 2-го слота),
(имя N-ro слота: значение N-ro слота).

Ту же запись представим в виде таблицы, дополнив двумя столбцами.


В таблице дополнительные столбцы предназначены для описания типа слота и возможного присоединения к тому или иному слоту специальных процедур, что допускается в теории фреймов. В качестве значения слота может выступать имя другого фрейма; так образуют сети фреймов.
Различают фреймы-образцы, или прототипы, хранящиеся в базе знаний, и фреймы-экземпляры, которые создаются для отображения реальных ситуаций на основе поступающих данных.
Модель фрейма является достаточно универсальной, поскольку позволяет отобразить все многообразие знаний о мире через:

фреймы-с тру к туры, для обозначения объектов и понятий (заем, залог, вексель);

фреймы-роли (менеджер, кассир, клиент);

фр еймы-сце н ар и и (банкротство, собрание акционеров, празднование именин);

фреймы-ситуации (тревога, авария, рабочий режим устройства) и др.
Важнейшим свойством теории фреймов является заимствованное из теории семантических сетей наследование свойств. И во фреймах, и в семантических сетях наследование происходит по АКО-связям (A-Kind-Of = это). Слот АКО указывает на фрейм более высокого уровня иерархии, откуда неявно наследуются, т.е. переносятся, значения аналогичных слотов.
Например, в сети фреймов на рисунке понятие "ученик" наследует свойства фреймов "ребенок" и "человек", которые находятся на более высоком уровне иерархии. Так, на вопрос: "Любят ли ученики сладкое?" Следует ответ: "Да", так как этим свойством обладают все дети, что указано во фрейме "ребенок". Наследование свойств может быть частичным, так, возраст для учеников не наследуется из фрейма "ребенок", поскольку указан явно в своем собственном фрейме.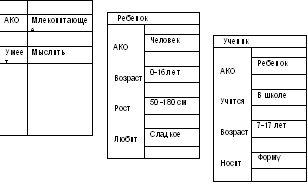
Основным преимуществом фреймов как модели представления знаний является способность отражать концептуальную основу организации памяти человека, а также ее гибкость и наглядность.
Специальные языки представления знаний в сетях фреймов FRL (Frame Representation Language) и другие позволяют эффективно строить промышленные ЭС. Широко известны такие фреймо-ориентированные экспертные системы, как ANALYST, МОДИС.

Формальные логические модели

Традиционно в представлении знаний вьщеляют формальные логические модели, основанные на классическом исчислении предикатов I порядка, когда предметная область или задача описывается в виде набора аксиом. Мы же опустим описание этих моделей по следующим причинам. Исчисление предикатов I порядка в промышленных экспертных системах практически не используется. Эта логическая модель применима в основном в исследовательских "игрушечных" системах, так как предъявляет очень высокие требования и ограничения к предметной области.
В промышленных же экспертных системах используются различные ее модификации и расширения, изложение которых выходит за рамки данного материала.